Pythonや統計を効率よく学ぶには？

AI・データサイエンス、
機械学習の実践力を高めたい方へ

プログラミングを0から学びたい
データサイエンティスト、データ
アナリストを目指したい
AIエンジニア、大規模言語モデル(LLM)エンジニアを目指したい

AI人材コースを無料体験してみませんか？

無料で120以上の教材を学び放題！
Pythonやデータ分析、機械学習など
AI人材に必須のスキルを無料体験できる！
データ分析、AI開発の一連の流れを体験、実務につながる基礎スキルを習得！

1分で簡単！無料！

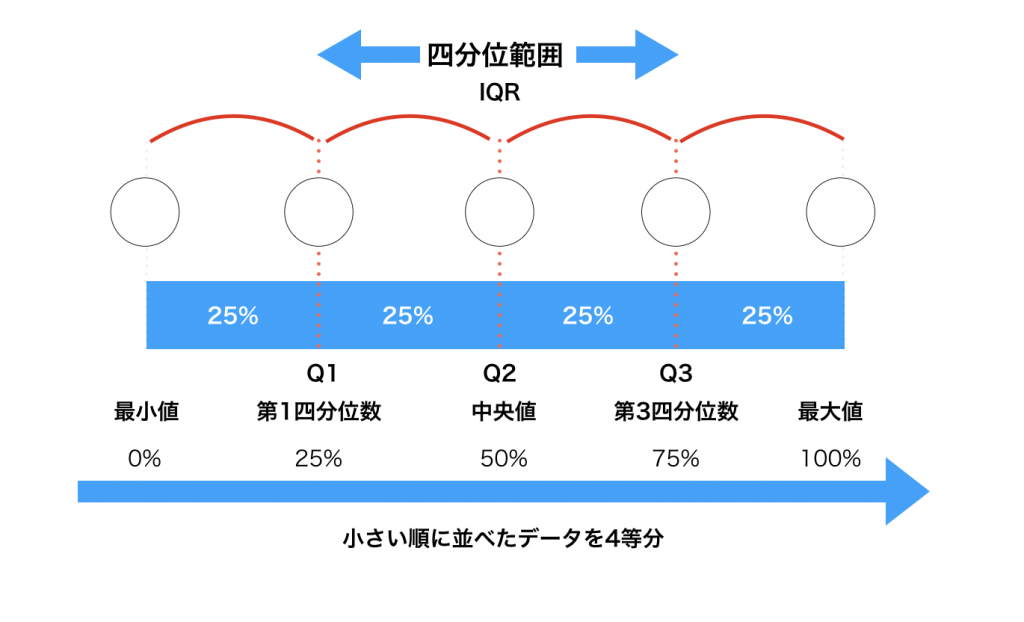
無料体験して特典を受け取る

四分位範囲とは

四分位範囲（IQR / Interquartile range）とは、75パーセンタイル（第3四分位数、Q3）から25パーセンタイル（第1四分位数、Q1）を引いた値です。データのちらばり具合を求めることが出来ます。

四分位範囲の算出方法は、Q3-Q1（第三四分位数　−　第一四分位数）で計算することが出来ます。

四分位範囲はいつ使うのか

四分位範囲は、データのバラツキを比較したい場合に利用します。

四分位範囲が大きい場合は、データのバラツキ具合も大きい（データの散らばりが大きいデータ）といえます。小さい場合は、データのばらつきが小さい（データが集中している）といえます。

また、四分位範囲は外れ値があっても、外れ値の影響を受けにくいため、中心付近のバラツキを表現できます。

Pythonで四分位範囲を求める

Pythonで四分位範囲を求めるには、いくつか方法がありますが、

今回は、numpyのnp.percentileを用いたサンプルプログラムを紹介いたします。

import numpy as np

sample_data = [1, 3, 5, 6, 300]

# 四分位範囲を求める
q1 = np.percentile(sample_data, 25)   # 第1四分位数
q2 = np.percentile(sample_data, 50)   # 第2四分位数（中央値）
q3 = np.percentile(sample_data, 75)   # 第3四分位数
iqr = q3 - q1 # 四分位範囲

# 結果を出力
print(f"第1四分位数: {q1}")
print(f"第2四分位数（中央値）: {q2}")
print(f"第3四分位数: {q3}")
print(f"四分位範囲: {iqr}")

出力結果

第1四分位数: 3.0
第2四分位数（中央値）: 5.0
第3四分位数: 6.0
四分位範囲: 3.0

上記のサンプルデータでは、ほとんどの値が6以下ですが、300という外れ値があっても、四分位範囲が

3であることがわかります。このようにばらつきを表す指標として、四分位範囲が活用できます。

Pythonや統計を効率よく学ぶには？

Pythonや統計を効率よく学ぶには、普段からPythonや統計学を用いて業務をしている現役のデータサイエンティストに質問できる環境で学ぶことです。
質問し放題かつ、体系的に学べる動画コンテンツでデータ分析技術を学びたい方は、オンラインで好きな時間に勉強できるAI Academy Bootcampがオススメです。受講料も業界最安値の35,000円（６ヶ月間質問し放題＋オリジナルの動画コンテンツ、テキストコンテンツの利用可能）なので、是非ご活用ください。