本記事は以下のテキストに移行しております。

https://aiacademy.jp/texts/show/?id=34&context=subject-metrics

はじめに

この章では機械学習の結果を評価する方法に関して説明します。
一部数式が出てきたりしますが、いきなり理解しようとせず、徐々に理解できるようになれば大丈夫です。
このテキストでは、Scikit-learnを用いて、評価の方法を学びますので、実際に手を動かしながら進めてみてください。

分類での評価方法

分類において使う主な評価指標は以下の通りです。
・混同行列（Confusion matrix）
・正解率(Accuracy)
・適合率（Precision）
・再現率（Recall）
・F値（F-measure）
一つずつ見ていきましょう。

混同行列とは

混同行列は二値分類（正事例と負事例の予測）の結果をまとめた表です。
分類結果を表形式にまとめることでどのラベルを正しく分類でき、どのラベルを誤って分類したかを調べることが出来ます。
真の値と予測した値の組み合わせには、それぞれ名称があり以下の図ように呼ばれます。
※下の混同行列では縦軸と横軸は以下の画像のようになっていますが、他の文献等では逆になっている場合もあります。どちらの混同行列の形でも読めるようにしましょう。

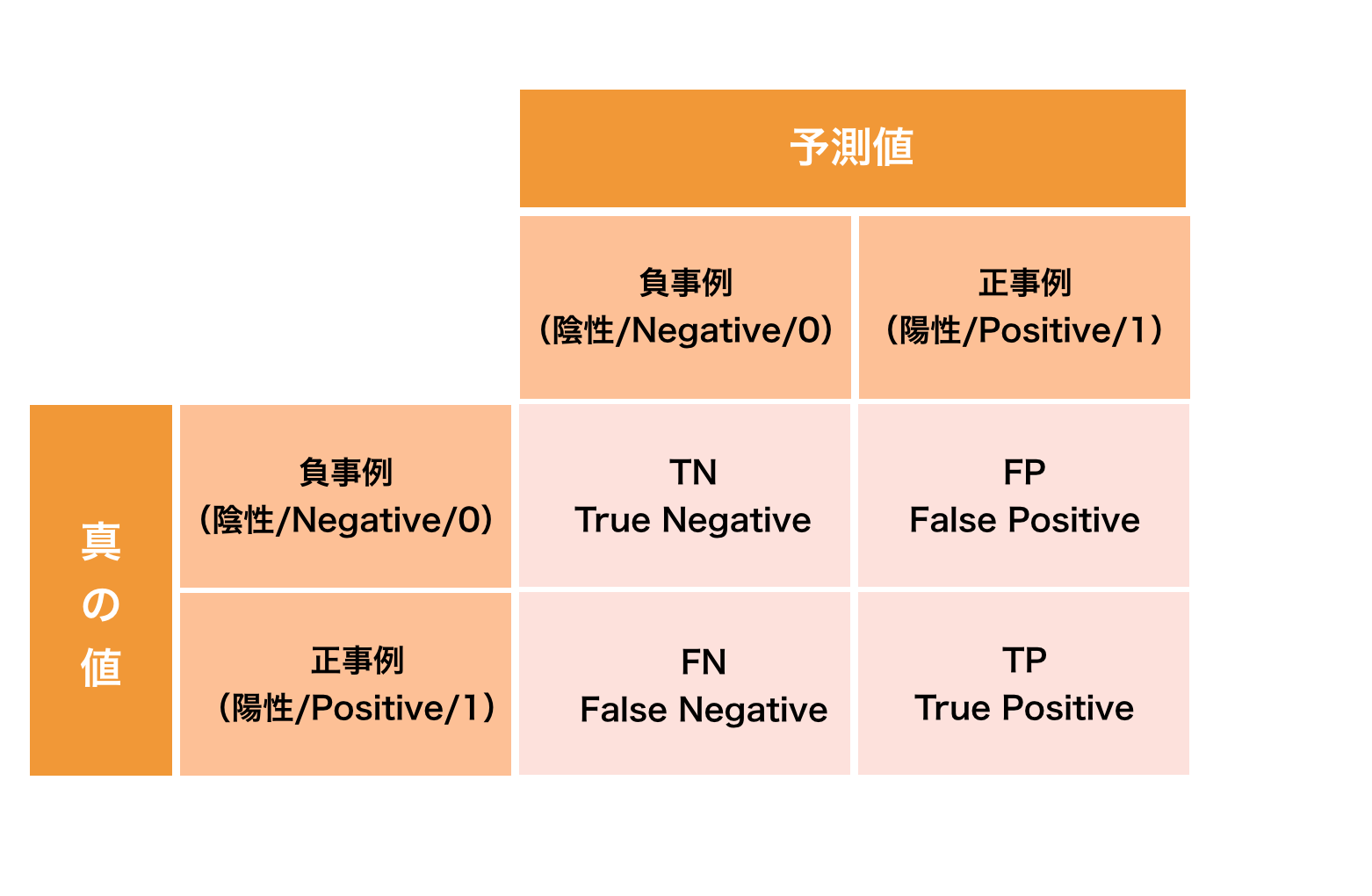
True Positive(TP) ・・・真の値が正事例のものに対して、正事例と予測したもの (真陽性)

False Positive(FP) ・・・真の値が負事例のものに対して、正事例と予測したもの(偽陽性)

False Negative(FN) ・・・真の値が正事例のものに対して、負事例と予測したもの(偽陰性)

True Negative(TN) ・・・真の値が負事例のものに対して、負事例と予測したもの(真陰性)

このTP、FP、FN、TNの値を可視化したものが混同行列です。
プログラムを入力して、混同行列をみてみましょう。
まず、データを作成します。

y_test = [0,0,0,0,0,1,1,1,1,1] # 0をNegative 1をPositiveとする
y_pred = [0,1,0,0,0,0,0,1,1,1]

y_testは真の値、y_predは機械学習によって予測した値だと考えてください。
また0を陰性（Negative）、1を陽性（Positive）とすると以下のような対応関係になります。

0 = Negative, 1 = Positive

          　　　Predicted
        　　　　　 0    　　　　　　1
Actual 0  TN   　　FP
　　　　　　　　　　　1  　FN　　　　　TP

次に、scikit-learnのconfusion_matrixによって混同行列を可視化します。

from sklearn.metrics import confusion_matrix

cmatrix = confusion_matrix(y_test,y_pred)
print(cmatrix )

実行すると、以下が出力されます。

[[4 1]
[2 3]]

それぞれの値を取得してみます。

tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel() #　混同行列のそれぞれの結果を取得
print("TN", tn)
print("FP", fp)
print("FN", fn)
print("TP", tp)

出力結果は以下のようになります。

TN 4
FP 1
FN 2
TP 3

正解率(Accuracy)

正解率とは、予測結果全体がどれくらい真の値と一致しているかを表す指標です。
以下の式で求められます。

$$
Accuracy = \displaystyle\frac{TP+TN}{TP+FP+FN+TN}
$$

正解率は、accuracy_scoreで求めることができます。

from sklearn.metrics import accuracy_score
print('Accuracy:',accuracy_score(y_test,y_pred))

実行すると、次のような値が出力されます。

Accuracy: 0.7

上のAccuracyの式のように、次のようにしても同じ出力になります。

tp, fn, fp, tn = confusion_matrix(y_test, y_pred).ravel() 
print((tp + tn) / (tp + fp + fn + tn))　# 0.7

注意すべき点は、正解率が高ければよいモデルというわけではないということです。
例えば、
真の値が[1, 1, 1, 1, 1, 1, 1, 1, 1, 0]
と負事例が1つのものだとします。
機械学習をした結果、
予測の値が[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
となったとき正解率は90%と計算され一見よいモデルと思えます。
しかし、1個の負事例を予測できていないためこのモデルは意味がない可能性があります。
このように正事例と負事例が不均衡なデータに対し、正解率を使って評価するのは難しいため、正解率以外にも適合率や再現率などの様々な指標があります。

適合率（Precision）

適合率とは、正事例と予測したもののなかで真の値が正事例の割合を表す指標です。
（出力した結果がどの程度正解していたのかを表す指標）

以下の式で求めることができます。

$$
Precision = \displaystyle\frac{TP}{TP+FP}
$$

＊また適合率は精度とも呼ばれます。（このテキストでは適合率を表す場合、適合率と表記します。）
適合率は、precision_scoreで求めることが出来ます。

from sklearn.metrics import precision_score
print('Precision:', precision_score(y_test,y_pred)) # 0.75

再現率（Recall）

再現率とは、真の値が正事例のもののなかで正事例と予測した割合を表す指標です。
以下の式で求めることができます。

$$
Recall = \displaystyle\frac{TP}{TP + FN}
$$

再現率は、recall_scoreで求めることが出来ます。

from sklearn.metrics import recall_score
print('Recall:', recall_score(y_test,y_pred)) # 0.6

F値（F-measure）

適合率と再現率はトレードオフの関係にあるので、2つの指標をまとめた指標としてF値があります。
F値は、適合率と再現率の調和平均によって計算されます。

$$
F – measure = \displaystyle\frac{2Precision * Recall}{Precision + Recall}
$$

F値は、f1_scoreで求めることが出来ます。

from sklearn.metrics import f1_score
print('F1 score:', f1_score(y_test,y_pred)) # 0.67

また、以下のように適合率、再現率、F値はscikit-learnのclassification_reportによってまとめて計算する事もできます。

from sklearn.metrics import classification_report

print("Classification report")
print(classification_report(y_test, y_pred))

実行すると以下が出力され、計算ができていることが分かります。

Classification report
precision    recall  f1-score   support
0       0.67      0.80      0.73         5
1       0.75      0.60      0.67         5
avg / total       0.71      0.70      0.70        10

F値は、f1-scoreのavg/totalの部分ですのでこの場合0.70になります。