主成分分析（PCA）とは
データセットの次元が多いと、データ分析においても、機械学習においても計算コストが増え、データの様子が分かりにくくなります。
その解決策として、統計や機械学習の分野でよく使われる手法が、主成分分析（Principal Component Analysis：PCA）です。
主成分分析では、特徴量を抽出することによって、データセット内の特徴量を削減することが出来ます。
それによって、3次元以下に次元を削減することが出来れば、データを可視化することもできます。
主成分分析では、特徴量を「選択」するものではなく、新しい特徴量を「抽出」します。
ただし、ここでいう「抽出」とは非可逆的な（一度抽出したら、元のデータセットの特長量には戻らない）ものなので、いくらか失われる情報が出てきます。
主成分分析を理解する
主成分分析とは、データセットの次元を削減するために用いる手法ですが、主成分分析をした後の次元数を何個にしなければならない、といった規定はありません。
ですので、極論をいってしまえば、主成分分析を行った後の次元数が元のデータセットと同じ次元数でも問題は無いのです。
それでは次元削減できていないではないか、と感じる人も多くいるかもしれませんが、
イメージでいえば主成分分析では、次元の重要でないものを消すことも、消さないこともできるといったものです。
数多くある次元数の中から、「重要な次元」のみをピックアップすれば、次元を減らすことが出来ます。
主成分分析は教師なし学習なので、正解（ラベルや教師データ）がないため、分散によって次元の重要度を決めます。
分散は、データのばらつきを表す指標の一つなので、分散が大きければ大きいだけデータのバラつきは大きく、
分散が小さければ小さいだけデータのバラつきが小さいといえます。
すなわち、分散が大きければデータの値ごとの差も見つけやすく、分散が小さければ、データの値ごとの差が見つけにくいといえます。
よって、一番初めに新しく抽出する次元は、その次元に射影したデータの分散が最大になるように作成します。
たとえば、まず2次元のデータを考えるために、下のようなy=2x+1の一次関数を考えましょう。
プロットする点は (2,5),(3,7),(5,11),(7,15) で、これらの点をx軸y軸に射影してそれぞれの分散を求めます。
まず主成分分析をする前の分散について考えます。上の図のようにデータをx軸に射影したときの分散は3.69, y軸に射影したときの分散は14.75です。
さらに、設定した関数から、(2,5),(3,7),(5,11),(7,15)が相関していることは明らかです。
ここで、2次元から1次元への圧縮を考えます。新しい次元Z1は、以下のようなものです。
新しく抽出した次元に射影したデータの分散は、x軸やy軸へデータを射影した時よりも間隔（バラつき）が大きいため、分散が大きいことが分かります。
さらに、この次元に直行する新しい次元についても考えてみましょう。
この次元では、すべてのデータの間隔（バラつき）が０なので、情報が全く含まれていないことが分かります。
主成分分析とは、このような作業によって、2次元を1次元に抽出する作業の事をさします。
Scikit-learnを用いた主成分分析
先ほどのような主成分分析は、Pythonではどのように実装できるのでしょうか。
実際に、打ち込んでみましょう。
次のコードでは、y=2x+1上の (2,5),(3,7),(5,11),(7,15)のデータを主成分分析して、分析結果したものの散布図を表示します。
import numpy as np
from matplotlib import pyplot as plt
from sklearn.decomposition import PCA
# 標準化に関しては下記のテキストをご参考ください。
# https://aiacademy.jp/texts/show/?id=555&context=subject-ml_practice
from sklearn.preprocessing import StandardScaler
# グラフ描画サイズを設定します
plt.figure(figsize=(7, 4))
# y = 2x+1
data = np.array([[2, 5], [3, 7], [5,11],[7,15]])
# 標準化
sc = StandardScaler()
# 標準化させる値
data = sc.fit_transform(data)
# 主成分分析の実行
pca = PCA()
pca.fit(data)
# データを主成分に変換する
features = pca.transform(data)
# 主成分をプロットする
plt.scatter(features[:, 0], features[:, 1])
plt.title('principal component')
plt.xlabel('Z1')
plt.ylabel('Z2')
plt.savefig('PCA_sample1')
plt.show()
このように入力をすると、出力結果は以下のようになります。
第一主成分と、第二主成分
以上によって、主成分分析の概念は説明しましたが、多くのデータはy=2x+1のような一次関数上にあるわけではありません。
基本的にはデータセットには、分散が含まれていて一つの次元に収めることは出来ません。そういったときには幾つかの主成分を考えること求められます。
今回の主成分に最初に選ばれたZ1軸のような、射影したデータの分散が最大になるような軸を第一主成分といい、第一主成分と直行する軸の中で、軸上に射影したデータの分散が最大になる軸を第二主成分といいます。
ここで少しだけ、どのように主成分分析がScikit-Learnの中で行われているか、線形代数を用いてざっくりと手順を説明しておきます。
ただし、Scikit-Learnを用いれば数行で書くことが出来ます。
よって、Scikit-Learnによる主成分分析を使えれば良いという人は、この手順について深く理解する必要はありません。
1.変数x1,x2,x3,…,xpを標準化する
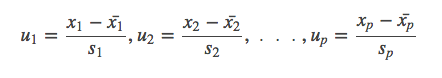
2.第一主成分ｚ１を以下のように定める
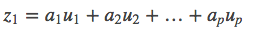
3.ｚ１の分散Vz1が最大になる[a1,a2,…,ap]を求める。
その解は各データのx1,x2,x3,…,xpの相関行Rとすると、
であり、第一固有値（最大固有値）λ1に対応する（長さ１の）固有ベクトルとなる。
このときVz1＝λ1となる
4.第二主成分はRの第２固有値λ2に対応する（長さ１の）固有ベクトルとなる。このときVz2＝λ2
5.第k主成分は第k固有値に対応する（長さ1の）固有ベクトルとして求める事が出来る。
この手順にのっとって第k主成分は、原理的には元の次元数pと同じ数まで増やすことが出来ます。
主成分分析の評価方法（累積寄与率）
原理的には元のデータの次元数まで増やすことのできる主成分ですが、いくつの主成分を採用すればよいのでしょうか。
一般的に累積寄与率が80%となるよう、主成分を抽出すると良いとされています。
ただし、この80％という数字はきちんと定められたものではなく、60％で良いという人もいます。
ですので、どの主成分を使うべきかについては、それぞれの分析者によって定められます。
第k主成分の寄与率の定義式は以下の通りです
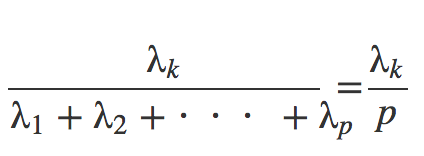
また、第k主成分までの累積寄与率を
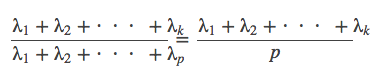
と定義する。
実際に、先ほどのy=2x+1の一次関数上に取った点での、各成分での寄与率と累積寄与率は、
explained_variance_ratio_メソッドを使うことで、計算することが出来ます。
先ほどのプログラムに以下のコードを追加してください。
print('各次元の寄与率: {0}'.format(pca.explained_variance_ratio_))
print('累積寄与率: {0}'.format(sum(pca.explained_variance_ratio_)))
# 出力結果
# 各次元の寄与率: [ 1.00000000e+00 1.36861370e-33]
# 累積寄与率: 1.0
実装例
実際に、どのように主成分分析が活用できるのか、今回はIrisデータセットを用いて考えてみましょう。
Iris（アヤメ）データセットとは、“setosa”, “versicolor”, “virginica” という 3 種類の品種のアヤメのがく片 (Sepal)、花弁 (Petal) の幅および長さを計測したデータです。
アイリスデータセットには150個のデータがあり、3種類のアヤメのデータがあるので、4次元のデータという事になります。
今回これら４次元のデータに関して主成分分析をすることで、2次元の第一主成分と第二主成分に抽出をし、可視化をします。
さらにそれらの累積寄与率を調べたいと思います。
まずはデータの読み込みをします
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
import matplotlib.cm as cm
# データセットの読み込み
iris = datasets.load_iris()
X = iris.data
Y = iris.target
# 主成分分析前のサイズ
print(X.shape)
Irisデータセットは3種類の150個のデータがある4次元のデータセットなので、出力は(150, 4)となります。
続いて、主成分分析によって、2次元に変換してみます。
# 主成分分析による次元削減
pca = PCA(n_components = 2, whiten = False)
pca.fit(X)
X_pca = pca.fit_transform(X)
print(X_pca.shape)
変換後にはIrisデータセットは150個のデータがある2次元のデータセットとなっているので、出力は(150, 2)となります。
さらに、このデータは2次元のデータなので、matplotlibを用いることで、これらを可視化することが出来ます。
# 分析結果を元にデータセットを主成分に変換する
transformed = pca.fit_transform(X)
# 主成分をプロットする
#花の種類別で色を変える
for label in np.unique(Y):
if label == 0:
c = "red"
elif label == 1:
c = "blue"
elif label == 2:
c = "green"
else:
pass
plt.scatter(transformed[Y == label, 0],
transformed[Y == label, 1],
c=c)
plt.title('principal component')
plt.xlabel('pc1')
plt.ylabel('pc2')
plt.show()
実行すると、以下のようなグラフが出力されます。
今回は第二主成分まで考えましたが、この累積寄与率を調べます。
累積寄与率が80％を大幅に超えているため、主成分分析の基準を満たしていると考えられます。
# 主成分の寄与率を出力します
print('各次元の寄与率: {0}'.format(pca.explained_variance_ratio_))
print('累積寄与率: {0}'.format(sum(pca.explained_variance_ratio_)))
# 出力結果
# 各次元の寄与率: [ 0.92461621 0.05301557]
# 累積寄与率: 0.9776317750248034
まとめ
Scikit-learnを活用した主成分分析を行いました。
まとめとして、Scikit-learnを用いた時の主成分分析の流れは以下の通りです。
1．主成分分析で次元削減を行う。
2．分析結果をもとに、データセットを主成分に変換する
3．主成分をプロットする
4．主成分の寄与率で基準を満たしているか評価する
ここでは、主成分の寄与率で、第k主成分の累積寄与率が80％であれば基準を満たすという表現をしましたが、その評価方法はケースバイケースで変化するので注意してください。
また、主成分分析の詳しいアルゴリズムについては、以下のURLが有効です。
30分で分かる次元削減
