AI・データサイエンス、
機械学習の実践力を高めたい方へ

• プログラミングを0から学びたい
• データサイエンティスト、データ
  アナリストを目指したい
• AIエンジニア、大規模言語モデル(LLM)エンジニアを目指したい

AI人材コースを無料体験してみませんか？

• 無料で120以上の教材を学び放題！
• Pythonやデータ分析、機械学習など
  AI人材に必須のスキルを無料体験できる！
• データ分析、AI開発の一連の流れを体験、実務につながる基礎スキルを習得！

1分で簡単！無料！

無料体験して特典を受け取る

赤池情報量基準（AIC）とは

AIC（Akaike’s Information Criterion / 赤池情報量基準）とは、モデルの当てはまり度合いを表す指標で、AICの値が小さいほど「よい」モデルとみなせる指標です。

一般的に以下の数式で表すことができます。

AIC = -2 ln(L) + 2k

• ln(L) は最大化された対数尤度
• k はモデルの自由度（パラメータ数）

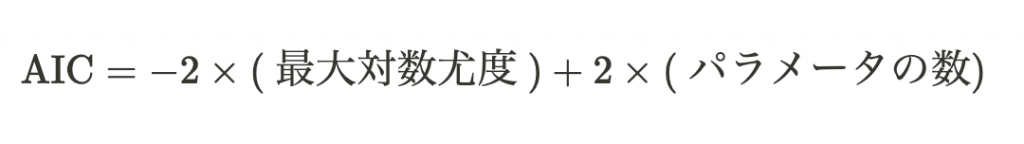
PythonでAICを計算する方法

Pythonでは、statsmodelsライブラリを使用して線形回帰モデルを適合させ、AICを計算することができます。

以下のコマンドで必要なライブラリをインストールしてください。

pip install statsmodels numpy

以下は、サンプルプログラムです。

import numpy as np
import statsmodels.api as sm

# データ生成
np.random.seed(0)  # 再現性のためのランダムシードを設定
X = np.random.rand(100, 1)  # 一様分布から100個のデータを生成（特徴量）
X = sm.add_constant(X)  # 定数項（バイアス、切片）を追加することで、回帰モデルにおける切片を推定可能にする
y = 3 * X[:, 1] + np.random.randn(100) * 0.5  # 真の関係式を設定し、ノイズを加えた目的変数を生成

# モデル適合
model = sm.OLS(y, X).fit()  # 最小二乗法（OLS: Ordinary Least Squares）で回帰モデルを適合させる

# AICの表示
print(f"AIC: {model.aic}")  # AIC（赤池情報量基準）を出力してモデルの適合度を評価

statsmodelsを用いることで簡潔にAICを計算することが可能です。モデル選択の際には、AIC以外の指標として、例えばBIC（ベイズ情報量基準）も併せて検討すると良いでしょう。

統計学や機械学習を効率よく学ぶには？

統計学や機械学習を効率よく学ぶには、普段からデータ解析している現役のデータサイエンティストや機械学習エンジニアに質問できる環境で学ぶことです。
質問し放題かつ、体系的に学べる動画コンテンツでデータ分析技術を学びたい方は、オンラインで好きな時間に勉強できるAI Academy Bootcampがオススメです。