【初心者向け】標準偏差とは何か？わかりやすく解説！

標準偏差とは

標準偏差とは、分散の平方根をとることによって計算される基本統計量の1つで、データの散らばりの度合いを示します。

標準偏差は以下の式で表されます。

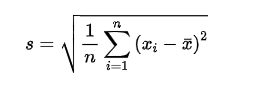
データの散らばりが大きいと標準偏差も大きくなります。また、散らばりが小さいと標準偏差は 0 に近づきます。文字式では、分散の文字式から２乗を取って、「s」や「σ」などと表されます。

標準偏差の求め方

標準偏差sを求めるには4つのステップを順に踏みます。

1. 平均値を求める
2. 偏差（数値－平均値）を求める
3. 分散（偏差の二乗平均）を求める
4. 分散の正の平方根を求める

標準偏差を求めるPythonプログラムは次のようになります。

scores = [90,80,40,60,90]

def mean(scores):
    s = sum(scores)
    N = len(scores)
    mean = s // N
    return mean

# 1. 平均値を求める
mean = mean(scores)

# 2. 偏差を求める
diff = []
for n in scores:
  # 一人一人のスコアから平均値を引いたものをdiffリストの末尾に追加。
  diff.append(n-mean)

print("偏差", diff)

# 3. 分散を求める
import numpy as np

# 分散(variance)
v = np.var(scores)
print("分散", v)

# 4. 分散の正の平方根を求める
std = np.std(scores)
print("標準偏差", std)

分散(variance)とは

分散とは数値データのばらつき具合を表すための指標です。分散は、偏差（それぞれの数値と平均値の差）を二乗し、平均を取ることで求められます。

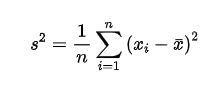
式を見ていただくと、分散は標準偏差を二乗した値になっています。

numpyのvar()を利用することで分散を表現できます。

import numpy as np

# 分散(variance)
v = np.var(scores)
print("分散", v) # 分散 376.0

scores = [90,80,40,60,90]
s = sum(scores)
N = len(scores)
mean = s // N

V1 = 0
for i in scores:
	V1 = V1 + (1/len(scores)) * (i - mean)**2

print(V1) # 376.0

出力結果